Thermodynamics of a VAE
Here is a description of the post
Introduction
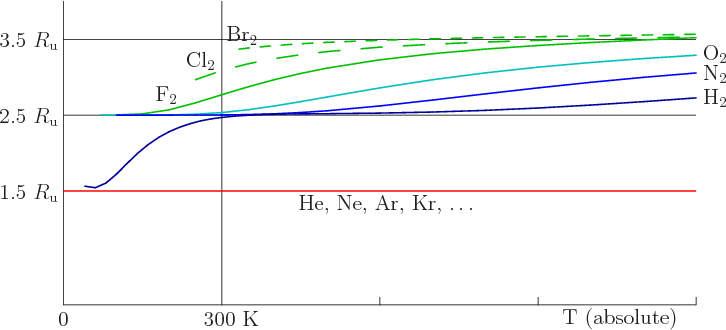
The equipartition theorem in Thermodynamics plays a central role in determining and understanding the behaviour of complex systems in thermodynamic equilibrium, linking bulk material properties with the detailed mechanics of the constituent parts. The role that it plays in determining the heat capacity of molecular gases played a central role in the fall of Classical physics and rise of Quantum physics in the late 19th and early 20th Century. The equiparition theorem basically states that the internal energy of a system in thermodynamic equilibrium is equally divided between its independent dynamical degrees of freedom, each degree of freedom getting \(T/2\) of energy, with the consequence that the heat capacity of a material basically amounts to counting the number of degrees of freedom. Classically, the heat capacity of a simple material like a diatomic gas of \(H_2\) could therefore be calculated as:
\[C = 7/2\]This follows from counting 7 degrees of freedom: 3 translational, 2 rotational, 2 vibrational. For a monatomic gas such as Helium, the result would be \(C=3/2\) from three translational degrees of freedom.